Как легко и просто решить СЛАУ

Как легко и просто решить СЛАУ? Почему важно уметь решать СЛАУ?

Системы линейных уравнений являются основой вычислительной математики, достаточно часто встречаются в различных алгоритмах решения задач. Применяются для решения всевозможных проблем  в физике, экономике и других науках. В задании № 20 ОГЭ также можно столкнуться со СЛАУ из двух уравнений.

Помочь разобраться в аспектах 20 задания можно на наших курсах подготовки к ОГЭ по математике, посещать которые можно очно или онлайн на нашем сайте.

Что такое СЛАУ?

Линейным уравнением называется уравнение, в котором переменные находятся в  первой степени. А системой линейных алгебраических уравнений – группа n линейных уравнений, содержащих k неизвестных. Её решением будет совокупность коэффициентов, при которой все уравнения обращаются в равенства.

Как решить СЛАУ?

Решение может быть нескольких видов:

• единственным;
• бесконечным множеством;
• отсутствовать.

Разберем основные приемы решения.

Метод подстановки

Вероятно,  этот метод знаком вам со школьной скамьи. Решение состоит из нескольких шагов:

1. Выразить из одного уравнения какое-либо неизвестное;
2. Подставить его в другое уравнение и получить ответ;
3. Решение подставить в первое уравнение и вычислить значение другого неизвестного.

Рассмотрим пример:

1. Выразим переменную из второго уравнения:

y = 5 – x

2. Подставим его в первое и получим х:

3. Подставим х во второе уравнение и получим у:

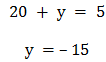
Решение (20,-15) получено!

Метод сложения (вычитания)

Этот метод тоже изучается в средней школе и весьма прост для восприятия. Алгоритм следующий:

1. Привести систему к виду, когда  коэффициент при какой-либо переменной имеет противоположные значения. Если такая ситуация уже присутствует в исходном уравнении, этот шаг разрешается исключить;
2. Сложить уравнения системы почленно, вследствие чего одно из неизвестных исчезает;
3. Решить полученное уравнение;
4. Подставить ответ в одно из первоначальных уравнений.

Рассмотрим ту же систему:

1. Домножим второе уравнение на -5:

2. Сложим уравнения системы почленно и сразу получим решение:

у = – 15

3. Подставим у во второе уравнение:

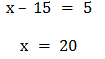
Мы повторно получили тот же ответ равный (20,-15)!

Метод Крамера

Этот метод употребляется в случае, когда число уравнений равно количеству неизвестных и основной детерминант матрицы не является нулем.

Определитель двумерной матрицы вычисляется таким образом:

a*d-b*c

Данную величину для трехмерной матрицы можно найти с помощью правила треугольника или разложения по строкам или столбцам.

Для метода Крамера потребуется главный определитель,  сформированный из показателей при неизвестных, и несколько вспомогательных, полученных заменой одного из столбцов главного определителя на столбец свободных членов.

Итак, последовательность действий:

1. Получить главный и вспомогательные детерминанты;
2. Используя формулы, получить значения неизвестных:

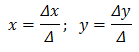
Продемонстрируем на известном нам примере:

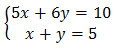
1. Составим матрицы и подсчитаем определители:

2. Воспользуемся формулами:

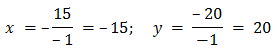
Выполнив вычисления, мы получили тот же ответ (20; -15), следовательно,  метод работает.

Метод обратной матрицы

Метод обратной матрицы также подразумевает, что основной определитель матрицы не равен нулю. Алгоритм действия такой:

1. Записать матричное уравнение;
2. Найти детерминант основной матрицы;
3. Вычислить обратную матрицу;
4. Умножить столбец свободных членов на обратную матрицу.

Для того, чтобы записать матричное соотношение, нужно выписать матрицу А (показатели  при переменных), столбец В (свободные члены) и столбец неизвестных.

Выразим Х:

Х = А^-1 * В

С помощью этого выражения мы и получим окончательный ответ.

Процесс нахождения определителя описан в предыдущем методе. Осталось научиться находить обратную матрицу по формуле:

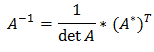
A^* называется матрица, скомпонованная из алгебраических дополнений, которые находятся через выражение следующего вида:

K – матрица, построенная после удаления строки n и столбца m.

A^T – транспонированная матрица. Для того чтобы ее вычислить, нужно всего лишь поменять местами строки  и столбцы.

Разберем  решение на знакомом примере:

1. Запишем матричное уравнение:

2. Определитель мы уже находили, он равен -1;
3. Вычислим обратную матрицу

• Найдем алгебраические дополнения:

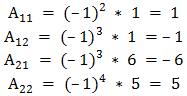
• Составим A^*:

• Вычислим A^T:

• Подставим в формулу обратной матрицы:

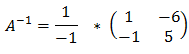
4. Перемножим значения по формуле:

Метод Гаусса

Метод Гаусса позволяет найти решение при любых условиях и параметрах, независимо от того, имеет ли матрица решение, и каким оно является. Способ заключается в преобразованиях, с помощью которых последовательно исключают переменные и приводят систему к виду, когда все неизвестные легко вычисляются с помощью подстановки. Рассмотрим алгоритм:

1. Запись расширенной матрицы и преобразование ее к виду трапеции;
2. Последовательное вычисление всех переменных, начиная с последнего уравнения.

Проиллюстрируем на примере:

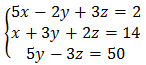
1. Запишем расширенную матрицу:

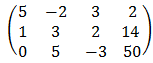
2. Вычтем из второй строки первую, умноженную на 1/5:

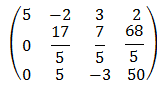
3. Вычтем из третьей строки вторую, умноженную на 25/17:

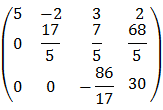
4. Решаем составленную систему:

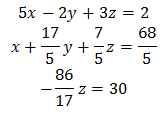
Получаем следующее решение:

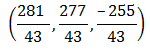
В этом материале мы рассмотрели различные методы решения СЛАУ. Теперь вы справитесь с этой задачей на отлично!

Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Остались вопросы? Задайте их эксперту!

Максим Муратов

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР

Задать вопрос

Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Кандидат физико-математичеких наук. Преподавательский стаж более 10 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.